圆台侧面积公式推导过程详细(圆台展开面积公式推导)

勾股定理大概是几何学里应用最为广泛的定理了吧。

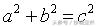
这个定理的表达式是如此的优美简洁，同时又是大部分几何定理推导中必须用到的基本定理，对于这个定理我最大的印象却是这个定理那些奇思妙想的证明，可以统计到的证法就有几百种，从遥远的毕达哥拉斯，到美国总统，又或是拿破仑大帝，都曾经贡献了证明。

本篇不赘述如此精彩的证明方法，决定从另一个方向来讨论这个美妙的结论，勾股定理有推广的情形吗？毫无疑问，先来看一个可能存在勾股定理表达类似的例子。

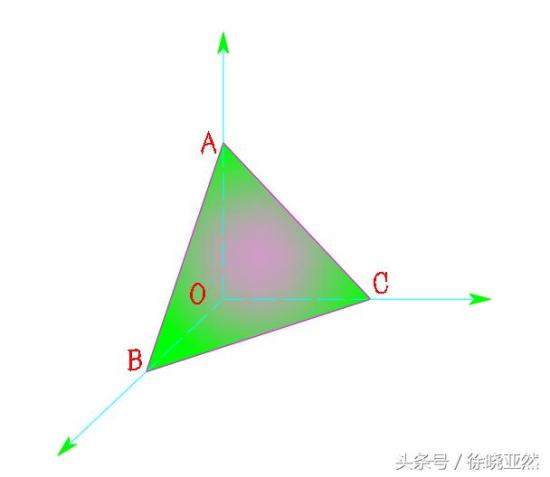
直角三棱锥

这里是一个空间坐标系，分别从x,y,z轴上取一点，于是，OABC构成了一个两两侧面垂直的三棱锥，这里与直角三角形的情形很类似，那么我们猜想，会不会有如下的结论呢？

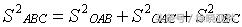
那么下面，我们来简要证明：

设0A=a,0B=b,OC=c;那么容易得到

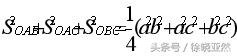
由于3个侧面都是互相垂直的直角三角形，可以得到

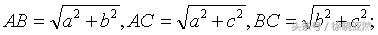
由公式

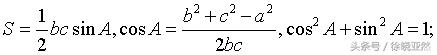
我们可以得到

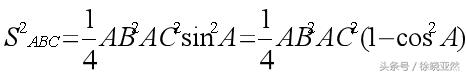
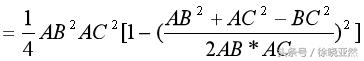
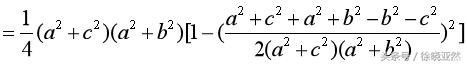
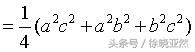
很幸运，与上面的计算结果完全一样，因此，勾股定理在垂直三棱锥的推广完全成立。

还有别的几何情况下的推广了么，想到另一种情况：直角三角形的一条直角边绕着直线旋转一周，每条边形成的区域面积是否也满足上述等式呢？

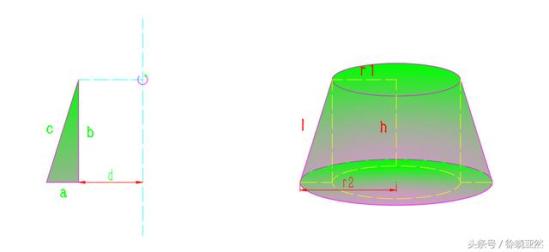
这里先考虑第一种情况，旋转轴与直角边平行：

这里b旋转面是矩形，a旋转面是圆环，c旋转面为扇环。根据圆台侧面积的计算公式

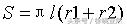
对于本图里的例子，r1=d,r2=a d,l=c;那么

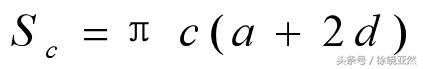
同样的

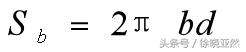
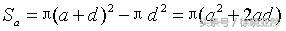
若存在

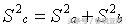
只需

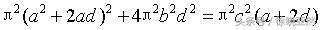
其中

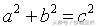
两式联立，可以得到

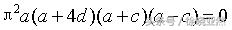
这里只有a=c时，上述等式才会成立，显然不可能，因此，上述推广情况下，任意直角三角形都不满足

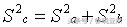
下面讨论直角三角形的斜边围绕直线一周的情况：

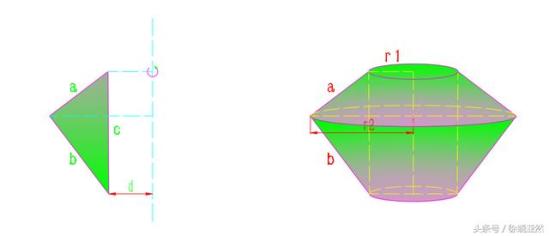
这里

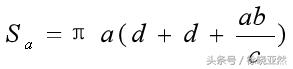
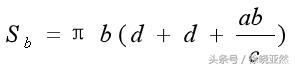
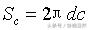
所以

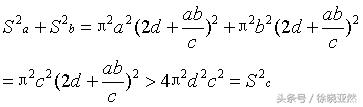
显然这种情况下，任何直角三角形也不会满足这个等式。

对于一些定理或者结论，发挥联想，进行与之相似性质的类比，往往会有特殊的收获。但是直觉也都不一定总是正确的，必须要经过严密的推理演绎才能将自己的猜想化成定理，比如本次勾股定理的第二种推广就通通不满足表达式。