协方差是指(协方差函数是干什么的)

离均差、方差、均方差、协方差这几个数学名词都听上去都差不多，可是在日常工作生活中能用得上这些概念的人应该不多，今天就来说说其中的差别。

要想搞清楚什么是离均差、方差、均方差和协方差，得先从均值这个概念开始。哪怕是数学再不好的人，也应该知道算术平均数是怎么回事吧。

以标准普尔500指数为例，在2018年9月10日至9月21日期间共有10个交易日，自然也就有10个标准普尔500指数的收盘价。将这10个交易日的标准普尔500指数收盘价相加后除以交易天数10，就会得出这10个交易日标准普尔500指数收盘价的均值2,902.46。

有了均值，下面就可以计算离均差，离均差就是一组数据中各个数值与该组数据均值的差异。用上述10个交易日的收盘价分别减去均值2,902.46，可以得出每一个收盘价的离均差。

离均差是计算方差的基础，将离均差乘方，相加求和后再除以10求平均值，得出来的结果就是这组数据的方差，方差衡量的也是一组数据中各个数值与该组数据均值的离散程度。在下表中，方差等于280.7405。方差的计算公式为

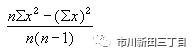
，其中x为样本平均值，n为样本的大小。

有了方差，标准差就迎刃而解了，因为标准差=方差的平方根，用σ表示。因此，前面这组数据的标准差=(280.7405)^(1/2)=16.7553。

且慢。。。以上的计算过程是基于该组数据是样本数据的总体这一前提假设，也就是说在标准普尔500指数的历史上只有2018年9月10日至9月21日这10个交易日的收盘价。当然这是不可能，因为这些数据只是抽样数据，是为了举例说明而给定的样本数据而不是数据的全部，因此需要对以上计算过程略作调整。上表中的和2,807.4055应除以（10-1）而不是10，方差的结果变成311.9339，同样标准差也就变成=(311.9339)^(1/2)=17.6617：

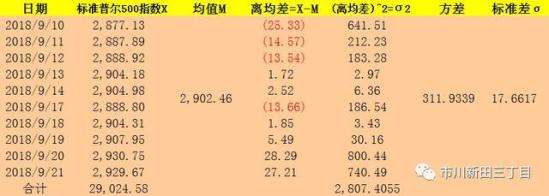
标准差又名均方差，是离均差平方的算术平均数的平方根，可用来衡量一组数据中各个数值与该组数据均值的离散程度。标准差的计算公式为

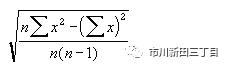
，其中x为样本平均值，n为样本的大小。标准差越大，说明该组数据中大部分数据与均值的差异较大。均值相等的两组数据，标准差却未必相同。比如，有A、B两组数据，如下表所示，这两组数据的均值都等于5。

但各数据偏离均值的程度是有差异的。。。，可以看到均值相等的两组数据中，A组中各个数据之间的差异程度要高于B组。

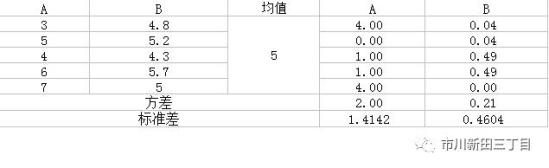
小结一下：方差是标准差的平方，是离均差平方的和的均值。

通过以上的演示计算，可以看到离均差、方差、标准差衡量的都是某一组数据内部各数值偏离均值的程度，通俗地讲是自己跟自己比。但下面介绍的协方差比较的是两组数据之间的差异程度。协方差的计算公式为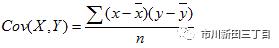其中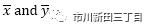

是两个数据系列的样本平均值，x、y为数据系列中的单个数据，n为样本的大小。

如果用于比较的两组数据完全相同，那么其方差和协方差的计算结果是一致的，因此方差只是协方差的一个特例。

有了方差和协方差，下一步就可以计算相关系数了，公式为

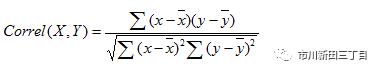
其中是两个数据系列的样本平均值，x、y为数据系列中的单个数据，n为样本的大小。

需要注意，如果用协方差计算相关系数，协方差中的x、y假设为全体数据，因此协方差公式中的标准差计算时，需要除以n而不是n-1。

以西德克萨斯轻质原油和标准普尔500指数为例，计算其收益率之间的相关系数，收盘价取值日期为2018年9月10日至9月21日。

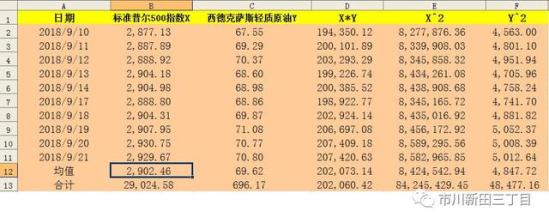
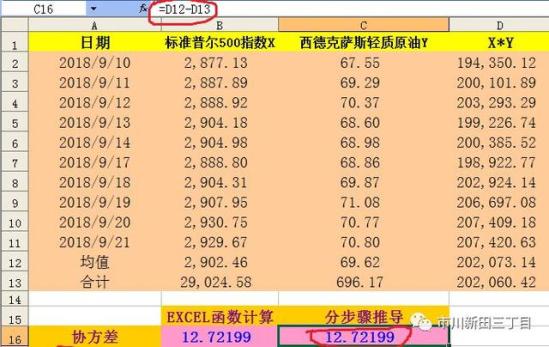
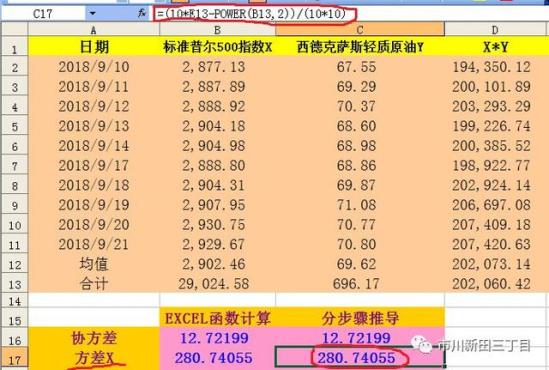
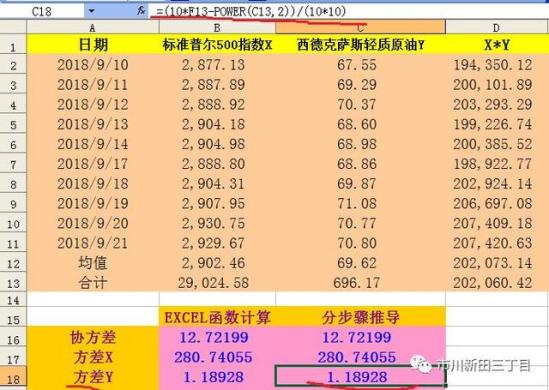
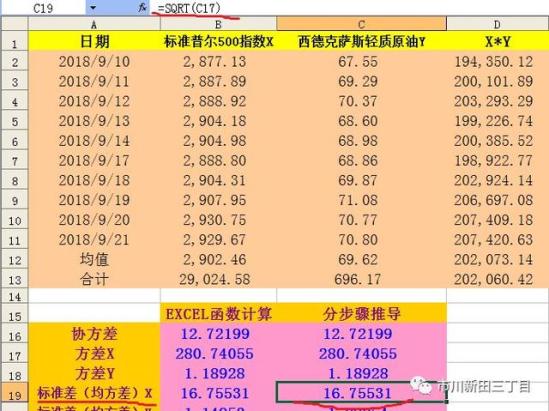
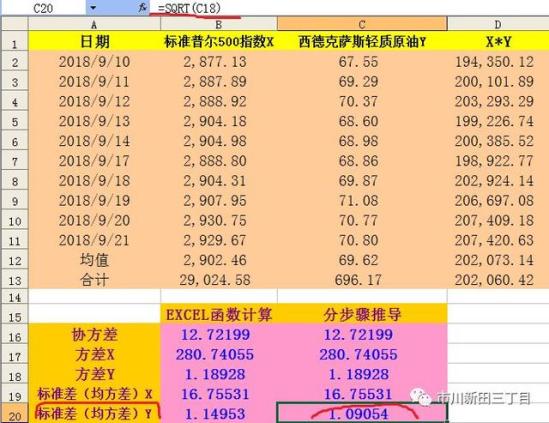
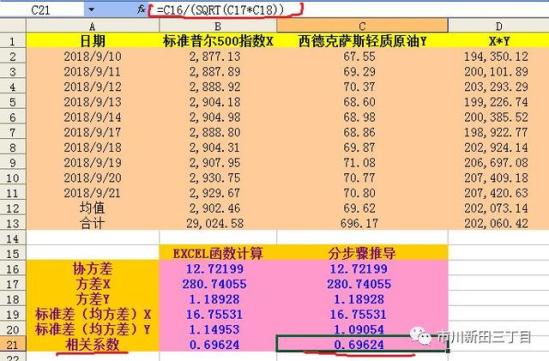
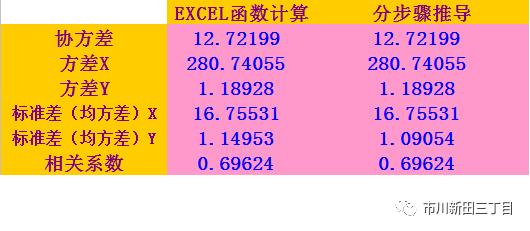
分布推导的结果与EXCEL自带函数计算结果相符。