重心的定义是什么(物体重心的定义及性质)

1.垂心：

〈1〉定义：是三角形三条高的交点。

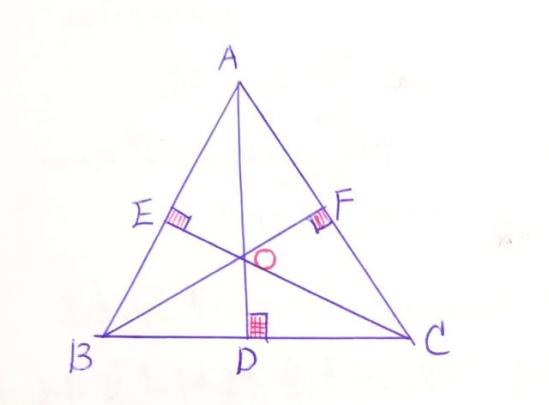
〈2〉性质：

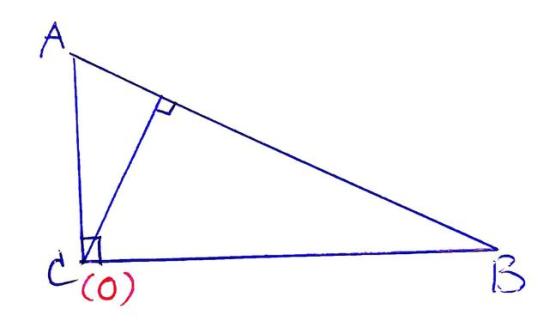
[性质1] 锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。

[性质2] 三角形的垂心是它垂足三角形的内心;或者说，三角形的内心是它旁心三角形的垂心。

[性质3] 垂心O关于三边的对称点，均在△ABC的外接圆圆上。

[性质4] △ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，。

[性质5]O、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为--垂心组)。

[性质6] △ABC，△ABO，△BCO，△ACO的外接圆是等圆。

[性质7] 三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。

[性质8]设O、 H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC, ∠BCO=∠HCA.

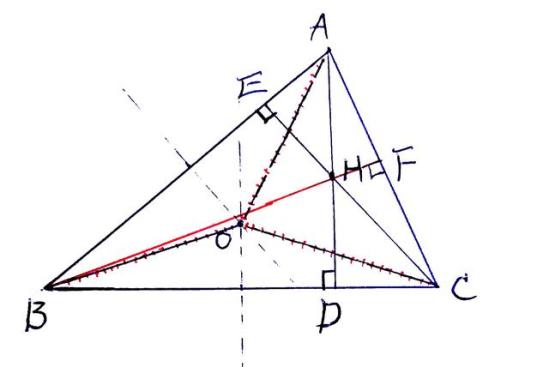
[性质9] 锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍，即 AH BH CH = 2（r R）。

[性质10] 锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。

[性质11] 设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA, AB.上的射影，H1,H2，H3分别为△AEF,△BDF，△CDE的垂心，则△DEF≌△H1 H2H3.

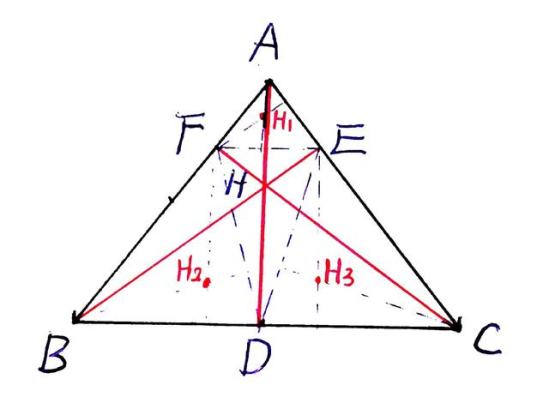
[性质12] 三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

2.内心

〈1〉定义：是三角形三条内角平分线的交点 即内接圆的圆心。

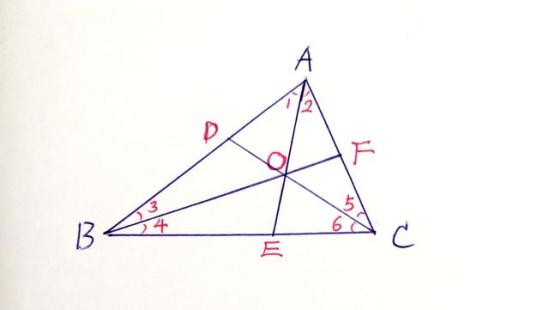
即AE、BF、CD分别平分角BAC、角ABC、角BCA，且AE、BF与CD相交于点O，点O即为△ABC的内心。

〈2〉性质：

[性质1] 三角形的内心到三边的距离相等,都等于内切圆半径r.

[性质2] ∠ BOC=90° ∠BAC/2。

[性质3] 在Rt△ABC中,∠A=90°,三角形内切圆切BC于D，则S△ABC=BDxCD

3.重心：

〈1〉重心的定义：重心是三角形三条中线的交点。

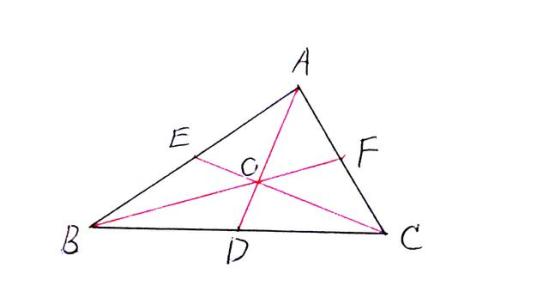
〈2〉重心的性质：

[性质1] 三角形的重心到边的中心与到这条边所对的顶点的距离之比为1:2，即OD：OA = 1：2 ；

OE：OC = 1：2 ；

OF：OB = 1：2 。

[性质2] 重心和三角形3个顶点组成的3个三角形面积相等，即S△AOB=S△BOC=S△AOC。即重心到三条边的距离与三条边的长成反比。

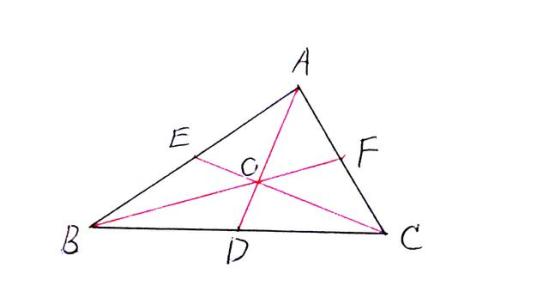
[性质3] 重心到三角形3个顶点距离的平方和最小。

[性质4] 在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数。即在△ABC中，若点A（X1、Y1）、B（X2、Y2）、C（X3、Y3），则其重心点O的坐标为{（X1 Ⅹ2 X3）/3、（Y1 Y2 Y3）/3}。

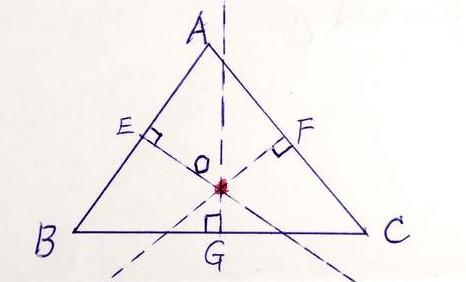
4.外心：

〈1〉外心的定义：外心是三角形三条边的垂直平分线的交点， 即外接圆的圆心。

〈2〉外心的性质：

[性质1] 若O是△ABC的外心,则∠BOC=2∠A（∠A为锐角或直角）或∠BOC=360°-2∠A（∠A为钝角）。

[性质2] 当三角形为锐角三角形时,外心在三角形内部；当三角形为钝角三角形时,外心在三角形外部；当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。

[性质3] 外心到三顶点的距离相等，即OA=OB=OC。

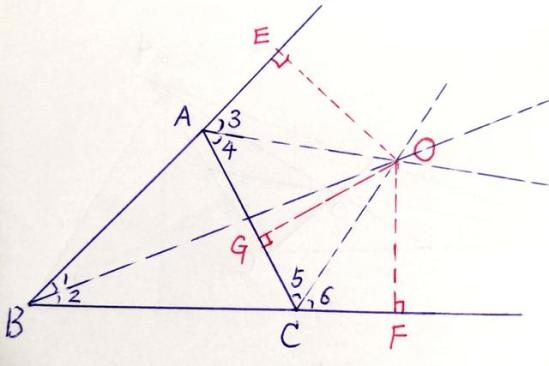
5.旁心：

〈1〉旁心的定义：

是三角形两条外角平分线和一条内角平分线的交点。

〈2〉旁心的性质：

[性质1] 旁心到三角形三边的距离相等，即OE=OF=OG。

[性质2]任何三角形都有3个旁心，且不相邻的内角平分线过旁心。

[性质3] 任意一个三角形都有三个旁切圆，三个旁心。旁心一定在三角形外。即⊙O1、⊙O2、⊙O3是△ABC的三个旁切圆， 〇1、〇2、〇3是△ABC的3个旁心，它们都在△ABC的外部。

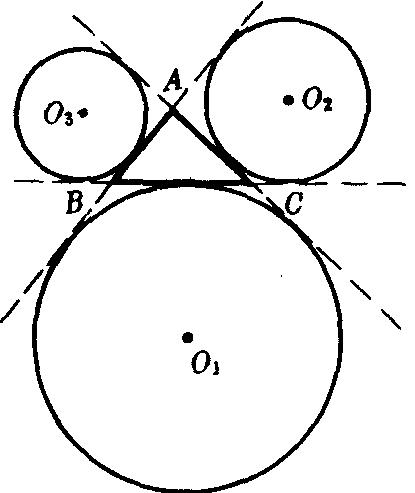
[性质3] 直角三角形斜边上的旁切圆的半径等于三角形周长的一半{假设△ABC是Rt△，且∠A=90度，⊙O1是斜边BC上的旁切圆，则此旁切圆的半径R1=1/2（AB BC AC）}。